توسط دیوید ریچسون
پارت پنجم
🔺 این پنج مرحله اول فرآیند هستند که منحنی پر کننده فضا را ایجاد می کنند. در هر مرحله منحنی صفر مساحت دارد ، اما در محدوده ، مربع را پر می کند. این منحنی خاص توسط دیوید هیلبرت معرفی شد.
این مثال و دیگر مثالهای شگفت انگیز به وضوح نشان داد که ریاضیدانان باید ثابت کنند که این ابعاد یک مفهوم واقعی است و به عنوان مثال ، فضاهای اقلیدسی n و m بعدی با درحالیکه m ≠ nمتفاوت هستند. این هدف به عنوان مشکل “تغییر ناپذیری بعد” شناخته شد.
سرانجام ، در سال ۱۹۱۲ ، تقریباً نیم قرن پس از کشف کانتور ، و پس از بسیاری از تلاشهای ناموفق برای اثبات تغییرناپذیری ابعاد ، براور با به کارگیری برخی از روشها موفق به ایجاد ابعاد شد. در اصل ، او ثابت کرد که غیرممکن است که جسمی با ابعاد بالاتر را در داخل ابعاد کوچکتر قرار داد ، یا ابعاد کوچکتر را در ابعاد بزرگتر قرار داد و کل فضا را پر کرد ، بدون این که جسم را به قطعات زیادی تقسیم کند. انجام داد ، یا اجازه داد که خود را قطع کند ، مانند Peano. علاوه بر این ، در این زمان براور و دیگران تعاریف گوناگونی دقیق ارائه کردند ، که به عنوان مثال ، می توانند بعد را به صورت استقرایی بر اساس این واقعیت که مرزهای توپ در فضای n-بعدی (n-1) بعدی است ، تعیین کنند.
اگرچه کار براور مفهوم ابعاد را بر پایه قوی ریاضی قرار داد ، اما در درک شهود ما در مورد فضاهای با ابعاد بالاتر کمکی نکرد: آشنایی ما با فضای سه بعدی به راحتی ما را به بیراهه می کشاند. همانطور که توماس بانچف نوشت ، “همه ما برده تعصبات ابعاد خود هستیم.”
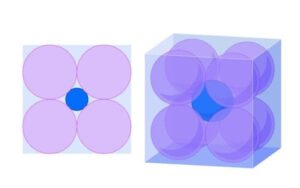
برای مثال ، فرض کنید ۲ ناحیه با شعاع ۱ را درون یک مکعب n بعدی با طول ضلع ۴ قرار می دهیم و سپس یکی دیگر را در مرکز مماس همه آنها قرار می دهیم. با افزایش n ، اندازه کره مرکزی نیز افزایش می یابد – شعاع آن ۱− √ − n است . بنابراین ، وقتی n ≥ ۱۰ این کره فراتر از کناره های مکعب بیرون زده است ، بسیار تکان دهنده است.
با افزایش بعد ، حوزه مرکزی بزرگتر می شود و سرانجام از جعبه بیرون می زند.